FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting 文献阅读
[TOC]
研究背景
长期时间序列预测在各种应用(例如,能源、天气、交通、经济等)中是一个长期存在的挑战。
尽管RNN类型的方法( Rangapuram et al., 2018; Flunkert et al., 2017）取得了令人印象深刻的结果，但它们经常遭受梯度消失或爆炸的问题（Pascanu et al., 2013)。极大地限制了它们的性能。继最近在NLP和CV社区((Vaswani et al., 2017; Devlin et al., 2019; Dosovitskiy et al., 2021; Rao et al., 2021)中取得成功之后，Transformer ( Vaswani et al , 2017)被引入到时间序列预测中捕捉长期依赖关系，并显示出有希望的结果( Zhou et al . , 2021 ; Wu et al , 2021)。由于较高的计算复杂度和内存需求使得Transformer难以应用于长序列建模，因此大量研究致力于降低Transformer(Li et al., 2019; Kitaev et al., 2020; Zhou et al., 2021; Wang et al., 2020; Xiong et al., 2021; Ma et al., 2021的计算成本。
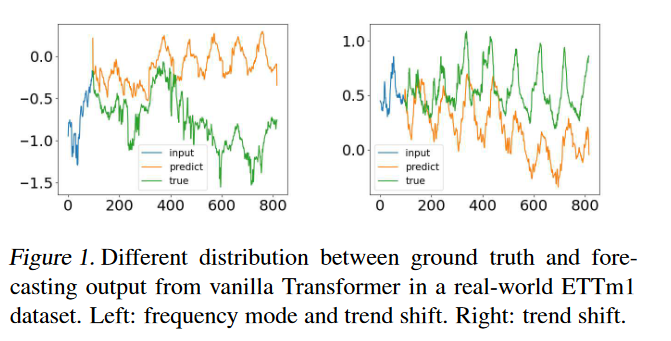
尽管基于Transformer的时间序列预测方法取得了一定的进展，但在某些情况下，它们往往无法捕获时间序列的整体特征/分布。在图1中，我们在一个真实的ETTm1数据集(Zhou et al., 2021).中比较了真实时间序列和vanilla Transformer方法(Vaswani et al., 2017)预测的真实时间序列。
显然，预测的时间序列具有与真实值不同的分布。真值和预测之间的差异可以用Transformer中的逐点注意和预测来解释。由于每个时间步的预测是单独独立进行的，模型很可能无法从整体上保持时间序列的全局性质和统计量。
创新点
为了解决每个时间步的预测是单独独立进行的，模型很可能无法从整体上保持时间序列的全局性质和统计量。本文在这项工作中采用了两种思路。
第一种思路是将时间序列分析中广泛使用的季节趋势分解方法(Cleveland et al., 1990; Wen et al., 2019),纳入Transformer - based方法。尽管这个想法在(Oreshkin et al., 2019; Wu et al., 2021)之前就已经得到了应用，但根据Kologrov-Smirnov分布测试，我们提出了一种特殊的网络设计，可以有效地使预测的分布接近真实值的分布。
第二个想法是结合傅里叶分析与基于变压器的方法。我们不是将Transformer应用于时域，而是将其应用于频域，这有助于Transformer更好地捕获时间序列的全局属性。
本文结合这两种思想，提出了一种用于长期时间序列预测的频率增强分解变换( Frequency Enhance Decomposition Transformer，简称FEDformer )。
模型结构
长期时间序列预测是一个序列到序列的问题。我们将输入长度记为I，输出长度记为O。我们将D记为序列的隐藏状态。编码器的输入是一个I × D矩阵，解码器有( I / 2 + O) × D输入。
FEDformer结构
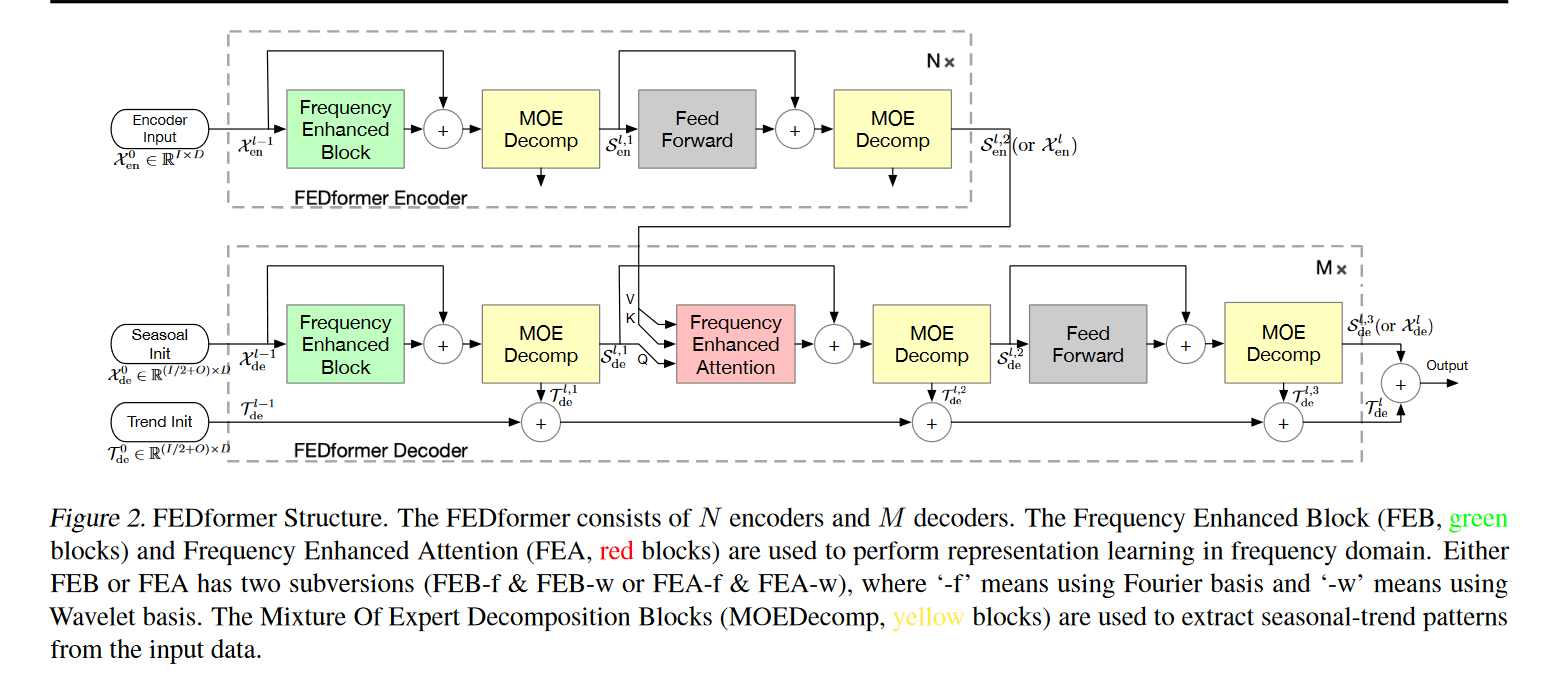
包括频率增强块( FEB )、连接编码器和解码器的频率增强注意力( FEA )和混合专家分解块( MOEDecomp )。
Frequency Enhanced Decomposition Architecture（频率增强分解结构）
在Autoformer中，分解模块使用的是固定的窗口大小，为了克服固定大小在具有复杂周期和趋势分量的现实情况下的不足，作者设计了一个混合型分解模块，其主要由若干个不同大小的窗口组成，提取到多个不同的分量特征，同时作者还对他们设置了权值，旨在区分不同分量特征对模型的贡献，最终以加权求和的方式获得最终趋势数据。这部分通俗易懂，主要进行了不同尺度的滤波操作获得多种结果，并对他们加权计算最终结果。
Fourier enhanced blocks and Wavelet enhanced blocks（傅里叶增强模块和小波增强模块）
在该部分，作者提出将Transformer和傅里叶分析相结合，取代以往将Transformer应用于时间特征提取，改为使用Transformer对傅里叶变换后的频域数据进行特征提取。然而时域数据转化为频域数据带来的是大量的频率分量，是否针对所有数据进行特征提取或者如何选择这些分量将是一个问题。针对这个问题，作者进行了分析和验证。
使用所有频率分量 虽然数据一点不会丢失，但考虑到傅里叶变换的局限性，过多的频率特征带来的将是冗余的信息资源、庞大的机器和时间开销以及过拟合的风险，因此不适用于对所有数据进行特征提取。
使用部分高频分量 高频分量代表时间序列中变化的突变型特征，确实具有一定的特殊性，然而噪声的存在否定了特殊性存在的合理性，过度地对高频分量进行特征提取，或许模型最终学习到更多噪声的内容，而难以关注时间序列本身。
使用部分低频分量 低频分量较为平缓，而时间序列中趋势的变化往往与重要事件的发生有关，缺少了高频分量对趋势的影响，时间序列将不具个性，预测的意义也大大降低。
随机选择分量 作者通过论证得到随机选取分量更有效，大大降低了复杂度。
该部分内容将被使用在时域转频域后频域分量的选择。
该部分借鉴自：https://blog.csdn.net/qq_43166192/article/details/130186788
编码器和解码器
编码器和解码器都采用多层结构
编码器
X^l^ en = Encoder(X^l-1^ en) , l∈{1，…….，N}表示第l个编码层的输出，X^0^ en∈R ^I×D^ 为嵌入的历史序列。
Encoder( )为：
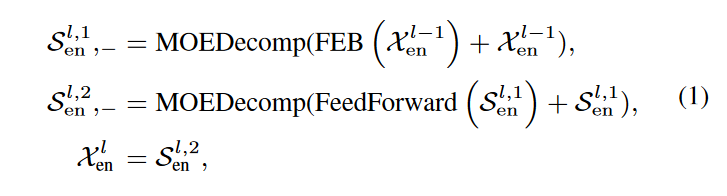
其中S^l,i^ en，i∈{ 1，2 }分别表示第l层第i个分解块后的季节分量。对于FEB模块，它有两个不同版本的( FEB-f & FEB-w)，分别通过离散傅里叶变换( DFT )和离散小波变换( DWT )机制实现，可以无缝替代自注意力模块。
解码器
X^l^ de, T^l^ de = Decoder(X^l-1^ de, T^l-1^ de ) 其中l∈{ 1，……，M }表示第l个解码层的输出。
Decoder( )表示为：
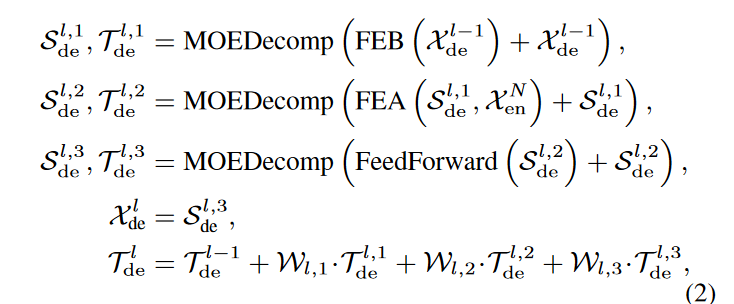
式中：S^l,i^ de, S^l,i^ de，i∈{ 1，2，3 }分别表示第l层第i个分解块后的季节分量和趋势分量
Wl,i ， i ∈ {1, 2, 3} 表示第i个被提取的趋势分量 T^l,i^ de
与FEB类似，FEA有两个不同的版本( FEA-f & FEA - w)，分别通过DFT和DWT投影实现，并带有注意力设计，可以替代交叉注意力模块。
最终的预测结果是两个细化分量之和WS · X ^M^ de + T^M^ de
其中WS 是为了将将深度变换后的季节分量X^M^ de 投影到目标维度。
模块结构分解
离散傅里叶变换（DFT）
令F表示傅里叶变换 ，F^-1^表示傅里叶逆变换。
给定一个时间域上的实数序列 xn 。
离散傅里叶变换公式为：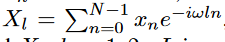
i为虚数单位
Xl ,l = 1，2 .. L是频域中的复数序列。
傅里叶逆变换公式为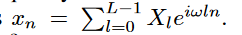
Frequency Enhanced Block with Fourier Transform (FEB-f)
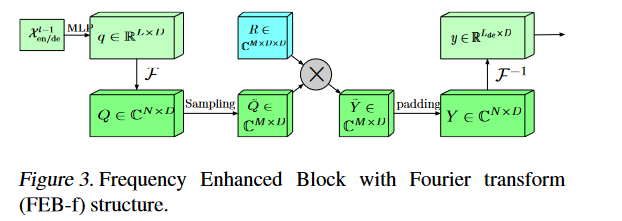
1、首先对输入X 运用多层感知机进行线性投影， 求得投影后的q , q = X*w
2、通过快速傅里叶变换，将时域数据q变为频域数据Q
3、对频域数据进行随机分量只保留随机选择的M个模态，减少信息冗余、降低增效
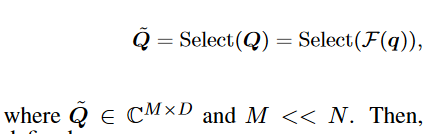
4、随机初始化矩阵R，并与随机选择的频率分量相乘；
令 $ Y = Q⊙C, Y_{m,d_o}=\sum_{d_i=o}^DQ_{m,d_i}·R_{d_i,d_o,m}$
$d_i= 1,2,3……D，d_o=1，2，3，……，D$
5、为了便于后续进行傅里叶逆变换，需要将数据以0补足维度；
6、通过傅里叶逆变换，由频域数据转换为时域数据。
Frequency Enhanced Attention with Fourier Transform (FEA-f)
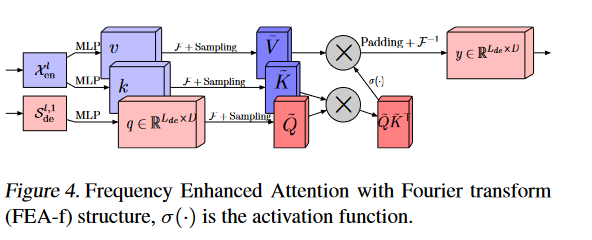
1、由Encoder经过多层感知机获得v和k，由Decoder经过多层感知机获得q
$q = x_{en} · w_q$ $k = x_{de}·w_k$ $v = x_{de}·w_v,$ $w_k, w_v ∈ R^{D×D}.$
2、 q 、k、v 在快速傅里叶变换下由时域数据转换为频域数据，对他们随机选择分量
3、接下来的步骤和传统注意力机制一样：k q相乘后经激活函数再与v相乘；
4、为了便于后续进行傅里叶逆变换，需要将数据以0补足维度；
5、通过傅里叶逆变换，由频域数据转换为时域数据。
小波变换
由于傅里叶变换存在明显的局限性：
它只能获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。
因此使用小波变换把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间了.
公式如下：
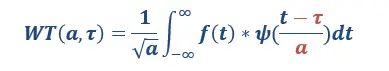
不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，平移量 τ控制小波函数的平移。尺度就对应于频率（反比），平移量 τ就对应于时间。（具体内容参考此文）
小波变化的频率增强块（FEB-w）
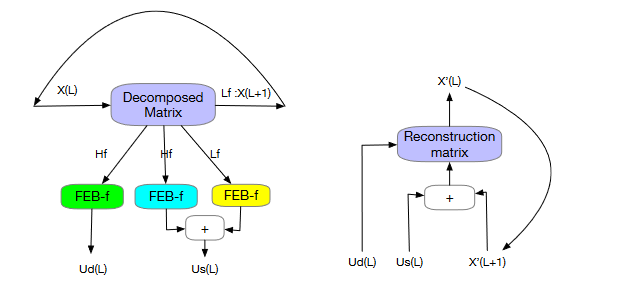
1、利用固定的Legendre小波基矩阵对输入值进行分解，得到高频、低频和剩余三个部分
2、运用FEB-f模块对三个部分分别处理。对于每个周期L，得出一个高频张量Ud(L)、低频张量Us(L)和原始低频张量X(L+1)
3、采用重建模块融合多组数据进行数据重建如右图所示。
对于每个循环L，将分解部分产生的X(L+1),Us(L)和Ud(L)进行组合，产生X(L)用于下一个重建循环
对于每个周期，信号张量的长度维度增加2倍
基于小波变换的频率增强注意力 (FEA-w)
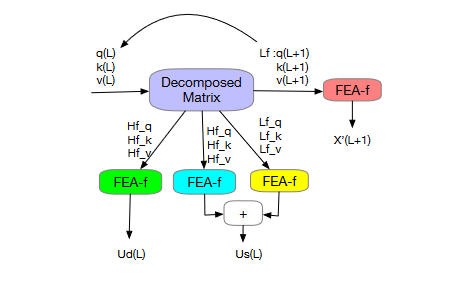
与FEB-w类似，使用相通的分解矩阵对k q v 分解为三对， 对每对q k v运用FEA-f进行特征提取。
最后再进行数据重构与FEB-w类似。
总结
Autoformer可以认为是将时序序列分解为多个时序子序列进行特征提取，而FEDformer则是从频域的角度进行提取，两个在具有相似模型框架的同时又有着较大的不同。通过多个实验，后者展现出优异的特征提取能力，进而在长时序中具有优异的性能。
作者在Autoformer的基础上进行深入创新，融入了傅里叶变换的同时，进一步探索了融入小波变换的可能性，更加证明了合理使用传统领域的发现，将其与深度学习相结合，往往会有着不错的效果。通过学习发现，小波变换部分的模块与傅里叶模块有着直接相关，因此小波模型的运行不管是空间还是时间都将是一大开销。
文章借鉴：