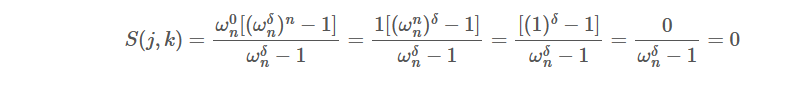离散傅里叶变换

离散傅里叶变换的作用

将时间域信号分解为构成它的频率成分，以此获得频率信息（振幅谱、功率谱和功率谱密度）可以获得我们无法从时间域获得的对信号的一些洞察。

离散傅里叶变换（DFT）便是帮助我们获得这些表示的第一步。

DFT将信号（时间域）或距离（空间域）转换到频率域。

可以通过转换找到原本域内不明显的信号特征

离散傅里叶变换的公式

$$
X_k = \sum_{n=0}^{N-1}{x_n}e^{-i\frac{2\pi}{N}kn}
$$

xn 为离散时间域信号 ✖ 复数为e的指数
$$
e^{-i\frac{2\pi}{N}kn} \
e^{-in} = cos(n)+isin(n)
$$
即可看作将时间信号✖特定频率的正弦和余弦，由变量k给出，再将结果求和。

可对不同的频率和不同的k值进行求和。

离散傅里叶变换仍旧是时域到频域的变换。由于求和形式的特殊性，可以有其他的解释方法。

如果把序列xn看作多项式f(x)的x^n^项系数，则计算得到的XK 恰好是多项式 f (x)代入单位根$e^{-i\frac{2\pi}{N}k} \$的点值$f(e^{-i\frac{2\pi}{N}k}\$）。

这便构成了卷积定理的另一种解释办法，即对多项式进行特殊的插值操作。离散傅里叶变换恰好是多项式在单位根处进行插值。

例如计算：

${n\choose 3} + {n\choose 7} +{n\choose 11}+{n\choose 15}+…… $

定义函数f(x)为：

$$f(x) = (1+x)^n = {n\choose 0}x^0 + {n\choose 1}x^1 +{n\choose 2}x^2+{n\choose 3}x^3+…… $$

然后可以发现，代入四次单位根 f(i)得到这样的序列：

$f(i) = (1+i)^n={n\choose 0} + {n\choose 1}i -{n\choose 2}x^2-{n\choose 3}i+……$

于是下面的求和恰好可以把其余各项消掉：

$f(1) + if(i) - f(-1) -if(-1) = 4{n\choose 3} + 4{n\choose 7} +4{n\choose 11}+4{n\choose 15}+…… $

因此这道数学题的答案为：

${n\choose 3} + {n\choose 7} +{n\choose 11}+{n\choose 15}+…… = \frac{2^n+i(1+i)^n-i(1-i)^n}4 $

这道数学题在单位根处插值，恰好构成离散傅里叶变换。

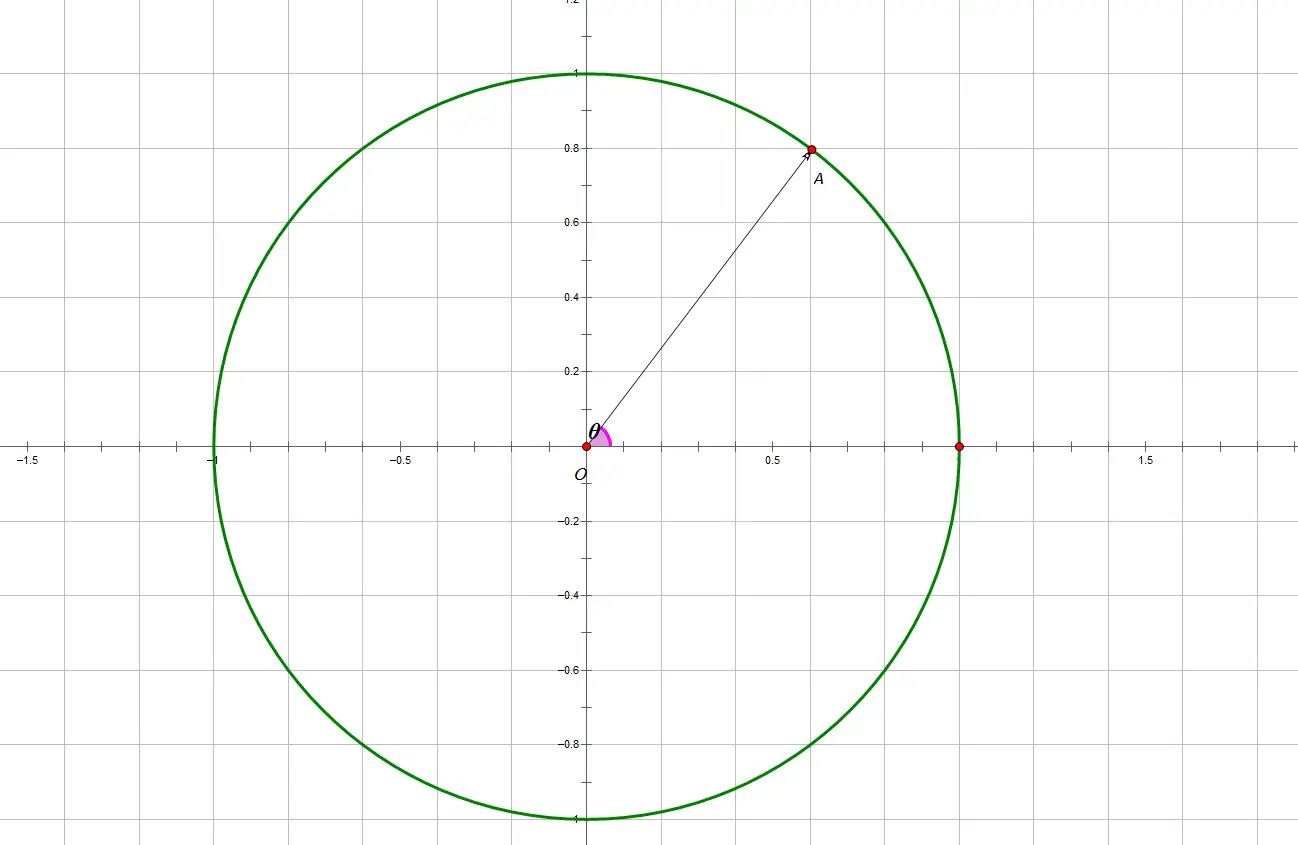
复平面中的单位圆

其中向量OA单位根，表示为 $e^i\theta$，可知 $e^i\theta = cos\theta+isin\theta$

将单位圆等分成 n个部分（以单位圆与实轴正半轴的交点一个等分点），以原点为起点，圆的这 n 个 n等分点为终点，作出 n个向量。

其中幅角为正且最小的向量称为 n次单位向量，记为$\omega_n^1 $。

其余的 n−1 个向量分别为$\omega_n^2,\omega_n^3,……，\omega_n^n$ ，它们可以由复数之间的乘法得来$\omega_n^k=\omega_n^k-*\omega_n^1$

易得 $\omega_n^n=\omega_n^0=1$

可把DFT看作时间信号和许多频率之间产生相关性

还可以看作矩阵乘法的旋转

X0 为时间信号与k=0 的内积以此类推

快速傅里叶变换（Fast Fourier Transform, FFT）

快速傅里叶变换 (Fast Fourier Transform, FFT) 是一种可在O(nlogn)时间内完成的离散傅里叶变换(Discrete Fourier transform, DFT) 算法.

傅里叶变换 (Fourier Transform) 本质上是信号与三角函数进行卷积运算，而快速傅里叶变换 (FFT) 就是提高卷积的计算效率，时间复杂度从 O(n^2^) 降低到 O(nlogn)

FFT 在算法中主要是用来在算法中的运用主要是用来加速多项式乘法或大数乘法

多项式乘法

考虑两个多项式 **A(x)，B(x) **，其乘积 **C(x) = A(x) * B(x) **

假设 A(x) 的项数为 n，其系数构成的 n维向量为 (a0,a1,a2,⋯,a~~n−1~~) ； B(x) 的项数为 m ，其系数构成的 m维向量为 (b0,b1,b2,⋯,b~~n−1~~)。

我们要求C(x) 的系数构成的n+m-1维的向量，先考虑暴力做法：

n = len(A)
m = len(B)
C = [0]*(m+n-1)
for i in range(n):
    for j in range(m):
        C[i+j] = A[i] * B[j]

可见时间复杂度是 O(n^2^) 。

实际运用中多项式的项数非常多，比如 10^5^ 这种级别，那么有没有什么方法可以加速运算呢？

已知在一组插值节点 (x^0^,x^1^,x^2^,⋯,x^n^)中，假设A(x)，B(x) 为多项式的项数相同。 **A(x)，B(x)**的点值向量分别为(ya0,ya1,ya2,⋯,yan) ，(yb0,yb1,yb2,⋯,ybn) ,则：

$A(x) = (x_0,y_{a0}),(x_1,y_{a1}),(x_2,y_{a2})，……，(x_n,y_{an})$

$B(x) = (x_0,y_{b0}),(x_1,y_{b1}),(x_2,y_{b2})，……，(x_n,y_{bn})$

$ C(x) =(x_0,y_{a0}·y_{b0}),(x_1,y_{a1}·y_{b1}),(x_2,y_{a2}·y_{b2})，……，(x_n,y_{an}·y_{bn}) $

那么 C(x) = A(x) ⋅ B(x) ，那么其点值表示法可以在 O(n) 的时间内求出

点值表示法
点值表示法是把这个多项式看成一个函数，从其中选取 n 个不同的点，从而利用这 n 个点来唯一地表示这个函数

设

$A(x_0) = y_0 = a_0 +a_1x_0+a_2x_0^2+a_3x_0^3+……+a_{n-1}x_0^{n-1}$

$A(x_1) = y_1 = a_0 +a_1x_1+a_2x_1^2+a_3x_1^3+……+a_{n-1}x_1^{n-1}$

$A(x_2) = y_2 = a_0 +a_1x_2+a_2x_2^2+a_3x_2^3+……+a_{n-1}x_2^{n-1}$

………………

$A(x_n) = y_n = a_0 +a_1x_n+a_2x_n^2+a_3x_n^3+……+a_{n-1}x_n^{n-1}$

那么用点值表示法表示 A(x) 如下：

$ A(x)= a_0 +a_1x+a_2x^2+a_3x^3+……+a_{n-1}x^{n-1} ⇔ A(x)=(x_0,y_{0}),(x_1,y_{1}),(x_2,y_{2})，……，(x_n,y_{n})$

可以观察到，多项式乘法的系数表示法就是做卷积运算，而点值表示法是做乘法运算。卷积定理告诉我们在一个域中的卷积相当于另一个域中的乘积。

在这里，系数表示法就是时域上表达，很复杂，而点值表示法就是频域上表示，就非常简单。那么我们将其转换为频域上表示，就可以大大降低其复杂度！

此时我们可以把快速傅里叶变换（FFT）看作是一个黑匣子，我们先向黑匣子输入A(x) ，B(x) ** 系数表达式，黑匣子内部先将A(x) ,B(x) ** 都变成点值表达式，黑匣子进行乘法运算后，再在内部转换为系数表达式.

FFT算法

FFT算法的基本思想是分治法，将多项式分为奇次项和偶次项处理

$ A(x)= a_0 +a_1x+a_2x^2+a_3x^3+……+a_{n-1}x^{n-1} $

按照次数的奇偶来分成两组，然后提出一个x:

$A(x) = (a_0 +a_2x^2+a_4x^4+a_6x^6……）+x(a_1 +a_3x^2+a_5x^4+a_7x^6)$

令

$H(x) = a_0 +a_2x+a_4x^2+a_6x^3+……+a_{n-2}x^{\frac{n-2}2}$

$G(x) = a_1 +a_3x+a_5x^2+a_6x^3+……+a_{n-1}x^{\frac{n-2}2}$

$A(x) = H(x^2)+xG(x^2)$

因为单位根$\omega_{2n}^{k+n}=-\omega_{2n}^k$ 即对于偶数次单位根$\omega_{n}^{k+n/2}=-\omega_{n}^k$ ,和$H(x^2)和G(x^2)$ 是偶函数，分别代如$\omega_{n}^{k+n/2}和\omega_{n}^k$ 可得到：

$$
A(\omega_{n}^k) = G((\omega_{n}^k)^2)+\omega_{n}^kH((\omega_{n}^k)^2) \
=G(\omega_{n}^{2k})+\omega_{n}^kH(\omega_{n}^{2k}) \
=G(\omega_{n/2}^k)+\omega_{n}^k*H(\omega_{n/2}^k))
$$
和
$$
A(\omega_{n}^{k+n/2}) =
G(\omega_{n}^{2k+n})+\omega_{n}^{k/2}H(\omega_{n}^{2k+n}) \
=G(\omega_{n/2}^k)-\omega_{n}^kH(\omega_{n/2}^k))
$$
因此我们求出了$G(\omega_{n/2}^k)和H(\omega_{n/2}^k)$后，就可以同时求出 $A(\omega_{n}^{k+n/2})和A(\omega_{n}^k) $。于是对G和H分别递归 DFT 即可。

离散傅里叶逆变换

用来实现上文黑匣子的另一半，将多项式点值表达式转换成系数表达式。

对于多项式$ A(x)= a_0 +a_1x+a_2x^2+a_3x^3+……+a_{n-1}x^{n-1} $ ，已知 n个点，其 n维点值向量为$ (A(x_0),A(x_1),A(x_2),……，A(x_n-1))$，请求解其n维系数向量 (a0,a1,a2,⋯,a~~n−1~~)？

1、设 (d0,d1,d2,⋯,d~~n−1~~)为 (a0,a1,a2,⋯,a~~n−1~~)得到的离散傅里叶变换的结果。

构造多项式：

$F(x) = d_0+d_1x+d_2x^2+……+d_{n-1}x^{n-1}$

2、设向量$（c_0,c_1,……,c_{n-1}）$,其中ck 为F(x) 在$x=\omega_{n}^{-k}$的点值表示，即

$$
c_k = \sum_{n=0}^{n-1}{d_i}(\omega_{n}^{-k})^i
$$

代入 $d_i = \sum_{j=0}^{n-1}{a_j}(\omega_{n}^{i})^j$得

$$
c_k = \sum_{n=0}^{n-1}{[\sum_{j=0}^{n-1}{a_j}(\omega_{n}^{i})^j]}(\omega_{n}^{-k})^i
$$

所以
$$
c_k = \sum_{j=0}^{n-1}a_j{\sum_{i=0}^{n-1}}(\omega_{n}^{i})^{j-k}
$$
令$S(j,k)={\sum_{i=0}^{n-1}}(\omega_{n}^{i})^{j-k}$,对其简化：

设$j-k=\delta$
$$
S(j,k)=\omega_{n}^{0}+\omega_{n}^{\delta}+\omega_{n}^{2\delta}+……+\omega_{n}^{(n-1)\delta}
$$
可见$\omega_{n}^{k}$为等比数列，其公比为$\omega_{n}^{\delta}$